I was recently documenting some DSP equations in Latex and couldn't find any suitable examples so I've put them together and thought I'd share.
The Fourier Transform
\large \mathscr{F} \normalsize (x(t))=\int_{-\infty}^{\infty}x(t)e^{-j \omega t}dt
Rendering
$$\large \mathscr{F} \normalsize (x(t))=\int_{-\infty}^{\infty}x(t)e^{-j \omega t}dt$$
The Discrete Time Fourier Transform
X(k) = \sum_{n=0}^{N-1}x(n).e^{-j 2 \pi nk/N},\; for\; 0 \le k \le N-1
Rendering
$$X(k) = \sum_{n=0}^{N-1}x(n).e^{-j 2 \pi nk/N},\; for\; 0 \le k \le N-1$$
The Inverse Discrete Time Fourier Transform
x(n) = \frac{1}{N} \sum_{k=0}^{N-1}X(k).e^{j 2 \pi nk/N},\; for\; 0 \le n \le N-1
Rendering
$$x(n) = \frac{1}{N} \sum_{k=0}^{N-1}X(k).e^{j 2 \pi nk/N},\; for\; 0 \le n \le N-1$$
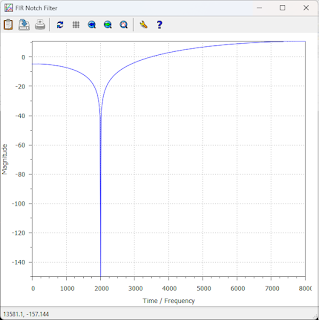
FIR Filter
y(n) = \sum_{n=0}^{N-1}h(k).x(n-k)
Rendering
$$y(n) = \sum_{n=0}^{N-1}h(k).x(n-k)$$
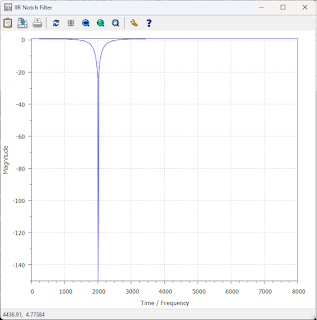
IIR Filter
y(n) = \sum_{k=0}^{N}a_{k}.y(n-k) + \sum_{r=0}^{M}b_{r}.x(n-r)
Rendering
$$y(n) = \sum_{k=0}^{N}a_{k}.y(n-k) + \sum_{r=0}^{M}b_{r}.x(n-r)$$
Roots Of Quadratic Equation $ax^{2} + bx + c = 0$
x=\frac{-b \pm \sqrt{b^2 - 4ac}}{2a}
Rendering
$$x=\frac{-b \pm \sqrt{b^2 - 4ac}}{2a}$$
One-Pole Filter
Difference Equation
y(n)=x(n)+\alpha.y(n-1)
Rendering
$$y(n)=x(n)+\alpha.y(n-1)$$
z Transform
Y(z)=X(z)+\alpha z^{-1}Y(z)
Rendering
$$Y(z)=X(z)+\alpha z^{-1}Y(z)$$
Transfer Function
H(z)=\frac{1}{1-\alpha z^{-1}}
Rendering
$$H(z)=\frac{1}{1-\alpha z^{-1}}$$
Frequency Response
H(e^{j\omega T})=\frac{1}{1-\alpha e^{-j\omega T}}
Rendering
$$H(e^{j\omega T})=\frac{1}{1-\alpha e^{-j\omega T}}$$
M-Point Moving Average Filter
Frequency Response
H[f]=\frac{sin(\pi f M)}{M sin(\pi f)} \: for \: 0 < f \leqslant 0.5
Rendering
$$H[f]=\frac{sin(\pi f M)}{M sin(\pi f)} \: for \: 0 < f \leqslant 0.5$$
Notes
\begin{equation*}
\begin{align*}
\end{align*}
\end{equation*}
VSCode doesn't support equation numbering auto increment and Colab doesn't support "equation*" or "aligned*" for disabling equation numbers. Colab requires "aligned" not "align".